Función inyectiva, sobreyectiva y biyectiva

Las funciones pueden tener diversas propiedades, las cuales facilitan su análisis y solución en muchos problemas de aplicación.

En mi publicación, el objetivo es aclarar la clasificación de las funciones que están presentes en los contenidos mínimos obligatorios de nuestro aprendizaje. Entre ellas está la función inyectiva, sobreyectiva y biyectiva.

Función Inyectiva.-

 

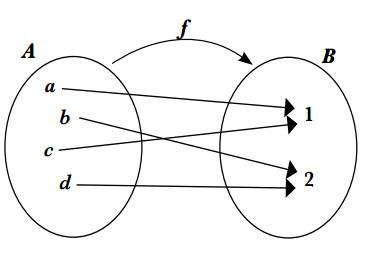
Una función \(f \) es inyectiva, o uno a uno,  de modo que los elementos distintos del dominio \(A\) le corresponden imágenes distintas en el codominio \(B\) .  Cada elemento de \(A\) tiene una única imagen en \(B\) (y sólo una). Se verifica que los elementos del conjunto  \(A\) siempre es menor o igual que los elemntos del conjunto \(B\). 

Algebraicamente una función inyectiva se define como; Si  \( f(x_{1}) = f(x_{2}), entonces, x_{1}= x_{2}\).

Veamos un contraejemplo:

En este caso, la función \(g\) no es inyectiva porque \(g(–1) = 1\) y \(g(1) = 1\), es decir, \(–1\) y \(1\) tienen la misma imagen.

Ahora analicemos geométricamente como la función \(f\) es infectiva y la función \(h\) no lo es. Simplemente se traza una recta paralela al eje \(x\) para determinar si una función es inyectiva o no. Si la recta corta en mas de 1 punto descartamos la posibilididad de que ella sea inyectiva.

 

En este caso, \(f\) no es inyectiva y \(g\) si lo es. 

Función Sobreyectiva.-

Una epiyección o sobreyección de \(A\) en \(B\) es toda función \(f\) de \(A\) en \(B\), de modo que todo elemento del codominio \(B\) es imagen de, al menos, un elemento del dominio \(A\). Cada elemento de \(B\) es imagen de por lo menos un elemento de \(A\). Se verifica que los elementos del conjunto \(A\) es mayor o igual a los elementos del conjunto \(B\). En otras palabras, en este caso el codominio es igual al recorrido.
Algebraicamente se define como;  \( \forall y \in Y\)   \( \exists x \in X  :  f(x)=y \)

Aquí un ejemplo y contraejemplo; \(f \) es sobreyectiva y \(g\) no lo es.

 

 La función \(f(x)=x+1\) es sobreyectiva.

Contraejemplo:

\( f(x) = x^2\)  No es Sobreyectiva.

Función Biyectiva.-

Una función es biyectiva si al mismo tiempo es inyectiva y sobreyectiva. Si cumple que sea Inyectiva y sobreyectiva a la vez, se verifica que la cardinalidad del conjunto \(A\) es igual a la cardinalidad del conjunto \(B\).
Algebraicamente la biyectividad se define como: \( \forall y \in Y\):   \( \exists !  x \in X  /  f(x)=y \)
Es decir, si para todo \(y\) de \(Y\) se cumple que existe un único \(x\) de \(X\), tal que la función evaluada en \(x\) es igual a \(y\).

 Ejemplos;
 \( f(x) = 2 – x\) es biyectiva.

Contraejemplo:
\( f(x) = x^2\)  No es biyectiva.