
La demostración de teoremas geométricos, en general, es un desafío para los estudiantes de enseñanza media, ya que deben establecer relaciones con otros conocimientos y teoremas, para posteriormente en una cadena lógica de argumentos llegar a demostrar nuevas proposiciones. A raíz de esto, trabajar con visualizaciones es un buen recurso para facilitar la comprensión en los estudiantes.
Entre los aprendizajes esperados de geometría para este nivel, existe una fuerte carga hacia la demostración de teoremas, entre ellos el de Euclides. En este caso los estudiantes deben establecer conexión con conocimientos previos tales como la semejanza de triángulos y el teorema de Thales. Justamente el desafío está en que recuerden y puedan aplicar dichos conocimientos, de lo contrario la demostración pierde sentido.
Para un buen desempeño de los estudiantes, la actividad supone que ellos ya han establecido el teorema particular de Thales (o teorema fundamental de semejanza), deben haber trabajado con relaciones proporcionales y tener claridad respecto de los elementos del triángulo rectángulo, en particular la altura y las proyecciones de los catetos sobre la hipotenusa.
1. Conocimientos Previos.
Entre los aprendizajes esperados de geometría para este nivel, existe una fuerte carga hacia la demostración de teoremas, entre ellos el de Euclides. En este caso los estudiantes deben establecer conexión con conocimientos previos tales como la semejanza de triángulos y el teorema de Thales. Justamente el desafío está en que recuerden y puedan aplicar dichos conocimientos, de lo contrario la demostración pierde sentido.
Para un buen desempeño de los estudiantes, la actividad supone que ellos ya han establecido el teorema particular de Thales (o teorema fundamental de semejanza), deben haber trabajado con relaciones proporcionales y tener claridad respecto de los elementos del triángulo rectángulo, en particular la altura y las proyecciones de los catetos sobre la hipotenusa.
1. Conocimientos Previos.
1.1 Suma de los ángulos interiores de un triángulo:
Se traza una paralela a la base por el
vértice opuesto.
El ángulo a’ = a, se dicen alternos
internos. El ángulo c’ = c por el mismo motivo.
a’ + b’ + c’ = 180°
Por lo tanto:
a + b + c =
180°
1.2 Triángulo rectángulo:
Definición: En geometría, se llama triángulo rectángulo a todo triángulo que posee un ángulo recto, es decir, un ángulo de 90-grados.
Se denomina hipotenusa al lado mayor del triángulo, el lado opuesto al ángulo recto. Se llaman catetos a los dos lados menores, los que conforman el ángulo recto.
Definición: En geometría, se llama triángulo rectángulo a todo triángulo que posee un ángulo recto, es decir, un ángulo de 90-grados.
Se denomina hipotenusa al lado mayor del triángulo, el lado opuesto al ángulo recto. Se llaman catetos a los dos lados menores, los que conforman el ángulo recto.
1.3 Teorema de Pitágoras:
 Definición: El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
Definición: El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
Si un triángulo rectángulo tiene catetos de longitudes \(a\) y \(b\), y la medida de la hipotenusa es \(c\) , se establece que:
 Definición: El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
Definición: El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).Si un triángulo rectángulo tiene catetos de longitudes \(a\) y \(b\), y la medida de la hipotenusa es \(c\) , se establece que:
$$a^{2}+b^{2}=c^{2}$$
1.4 Triángulos semejantes:
Definición: Dos triángulos son semejantes cuando tienen la misma forma, sus ángulos correspondientes son congruentes, sus lados proporcionales pero con distinta medida.
Notación: ~
Definición: Dos triángulos son semejantes cuando tienen la misma forma, sus ángulos correspondientes son congruentes, sus lados proporcionales pero con distinta medida.
Notación: ~
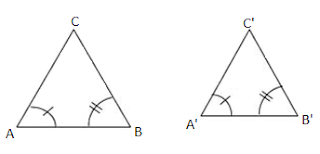 |
Sea \(< CAB= <C´A´B´\),
\(< ABC= <A´B´C´\) y \(< BCA= <B´C´A´\) y además
\(< ABC= <A´B´C´\) y \(< BCA= <B´C´A´\) y además
\(\dfrac {\overline {AB}} {A´B´}=\dfrac {\overline {BC}} {\overline {B´C´}}=\dfrac {\overline {CA}} {\overline {C´A´}}\)
entonces se puede decir que:
\(\Delta ABC\sim \Delta A´B´C´\)
\(\Delta ABC\sim \Delta A´B´C´\)
1.4.1 Criterios de Semejanza de Triángulos:
Para saber si dos triángulos son semejantes utilizamos algunos de los criterios de semejanza:
Criterio 1: “Ángulo – Ángulo” (AA)
Dos triángulos son semejantes cuando tienen dos de sus ángulos respectivamente congruentes.
Para saber si dos triángulos son semejantes utilizamos algunos de los criterios de semejanza:
Criterio 1: “Ángulo – Ángulo” (AA)
Dos triángulos son semejantes cuando tienen dos de sus ángulos respectivamente congruentes.
Hipótesis: \(<CAB = <C´A´B´\)
Tesis: \(\Delta ABC\sim \Delta A´B´C´\)
Demostración:
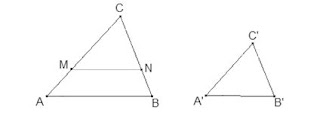
Se traza el segmento \(\overline {MN}\) tal que:
\(\overline {MN}\parallel \overline {AB}\)
Formádose el \(\Delta CMN\).
Luego en el \(\Delta MNC\) y \(\Delta A´B´C´\):
\(\overline {CM} = \overline {C´A´}\) / Por construcción
\(< BCA = < B´C´A´\) / Por hipótesis
\(< CMN = < CAB\) / Ángulos correspondientes entre \(\overline {MN}\parallel \overline {AB}\)
\(< CAB = < C´A´B´\) / Por hipótesis
Por lo tanto, \(< CMN = < C´A´B´\) / Por transitividad
Por lo tanto, \(\Delta MNC\) = \(\Delta A´B´C´\) (1) por tener un lado congruente y los dos ángulos adyacentes.
como \(\Delta ABC \sim \) \(\Delta MNC\) (2) Teorema fundamental de existencia
Comparando (1) y (2), tenemos:
\(\Delta ABC \sim \) \(\Delta A´B´C´\)
Criterio 2: “Lado – ángulo – lado” (LAL)
Dos triángulos son semejantes cuando tienen, respectivamente dos de sus lados proporcionales y el ángulo formado por ellos congruentes.
Hipótesis: Sea \(\Delta ABC\) = \(\Delta A´B´C´\).
\(< BCA = < B´C´A´\)
\(\dfrac {\overline {AC}} {A´C´}=\dfrac {\overline {BC}} {\overline {B´C´}}\)
Tesis: \(\Delta ABC \sim \)\(\Delta A´B´C´\)
Demostración: Tomando \(\overline {CM}=\overline {C´A´}\) y tracemos \(\overleftrightarrow {MN}\parallel \overleftrightarrow {AB}\), formádonse el \(\Delta MNC\).
En \(\Delta MNC\) y \(\Delta A´B´C´\):
\(\overline {CM}=\overline {C´A´}\) / (1) por construcción.
<BCA = <B´C´A´ / por hipotesis
En los \(\Delta ABC\) y \(\Delta MNC\)
\(\dfrac {\overline {AC}} {MC}=\dfrac {\overline {BC}} {\overline {NC}}\) / (2) por construccion \(\overline {CM}=\overline {C´A´}\)
Sustituyendo (1) en (2), tenemos lo siguiente:
\(\dfrac {\overline {AC}} {A´C´}=\dfrac {\overline {BC}} {\overline {NC}}\) / (3)
pero como: \(\dfrac {\overline {AC}} {A´C´}=\dfrac {\overline {BC}} {\overline {B´C´}}\) / (4) Hipotesis
Comparando (3) y (4):
\(\dfrac {\overline {BC}} {NC}=\dfrac {\overline {BC}} {\overline {B´C´}}\) / por Transitividad
Despejando \(\overline {NC}=\dfrac {\overline {BC}.\overline {B´C´}} {\overline {BC}}\)
\(\overline {NC}=\overline {B´C´}\)
\(.:\Delta MNC = \Delta A´B´C´\) / por tener dos lados congruentes e igual ángulo comprendido.
Y como \(\Delta ABC \sim \Delta MNC\) / teorema fundamental de existencia
y \(\Delta MNC \sim \Delta A´B´C´\) /carácter idéntico.
Resulta \(\Delta ABC \sim \Delta A´B´C´\) /por transitividad.
Criterio 3: “Lado – lado - lado” (LLL)
Dos triángulos son semejantes cuando tienen sus tres lados, respectivamente, proporcionales.
Hipótesis: Sean \(\Delta ABC\) y \(\Delta A´B´C´\)
\(\dfrac {\overline {AB}} {\overline {A´B´}}=\dfrac {\overline {BC}} {\overline {B´C´}}=\dfrac {\overline {CA}} {\overline {C´A´}}\)
Tesis: \(\Delta ABC \sim \Delta A´B´C´\)
Demostración: Tomando \(\overline {CM}=\overline {C´A´}\) y tracemos \(\overleftrightarrow {MN}\parallel \overleftrightarrow {AB}\), formando \(\Delta MNC \sim \Delta ABC\)
Como: \(\dfrac {\overline {AB}} {\overline {MN}}=\dfrac {\overline {BC}} {\overline {NC}}=\dfrac {\overline {CA}} {\overline {CM}}\) / (1) por construcion \(\Delta ABC \sim \Delta MNC\)
Pero: \(\overline {CM}=\overline {C´A´}\) / (2) por construccion
Sustituyendo (2) en (1);
\(\dfrac {\overline {AB}} {\overline {MN}}=\dfrac {\overline {BC}} {\overline {NC}}=\dfrac {\overline {CA}} {\overline {C´A´}}\) / (3)
Pero:
\(\dfrac {\overline {AB}} {\overline {A´B´}}=\dfrac {\overline {BC}} {\overline {B´C´}}=\dfrac {\overline {CA}} {\overline {C´A´}}\) / (4) por hipotesis
Comparando (3) y (4):
\(\dfrac {\overline {AB}} {\overline {MN}}=\dfrac {\overline {BC}} {\overline {NC}}=\dfrac {\overline {AB}} {\overline {A´B´}}=\dfrac {\overline {BC}} {\overline {B´C´}}\) / por transitividad
Despejando \(\overline {MN}\): \(\overline {MN}=\dfrac {\overline {AB}.\overline {A´M´}} {\overline {AB}}\)
\(\overline {MN}=\overline {A´B´}\)
Tomando la 3era y la 4ta razón:
\(\dfrac {\overline {BC}} {\overline {NC}}=\dfrac {\overline {BC}} {\overline {B´C´}}\)
Despejando: \(\overline {NC}\): \(\overline {NC}=\dfrac {\overline {BC}.\overline {B´C´}} {\overline {BC}}\)
\(\overline {NC}=\overline {B´C´}\)
Entonces \(\overline {MN}=\overline {A´B´}\), \(\overline {NC}=\overline {B´C´}\) y \(\overline {CM}=\overline {A´C´}\) / Por construccion
\(.:\Delta MNC = \Delta A´B´C´\) / Por tener 3 lados congruentes.
y como \(\Delta ABC \sim \Delta MNC\) /Por teorema fundamental.
Tesis: \(\Delta ABC\sim \Delta A´B´C´\)
Demostración:
Se traza el segmento \(\overline {MN}\) tal que:
\(\overline {MN}\parallel \overline {AB}\)
Formádose el \(\Delta CMN\).
Luego en el \(\Delta MNC\) y \(\Delta A´B´C´\):
\(\overline {CM} = \overline {C´A´}\) / Por construcción
\(< BCA = < B´C´A´\) / Por hipótesis
\(< CMN = < CAB\) / Ángulos correspondientes entre \(\overline {MN}\parallel \overline {AB}\)
\(< CAB = < C´A´B´\) / Por hipótesis
Por lo tanto, \(< CMN = < C´A´B´\) / Por transitividad
Por lo tanto, \(\Delta MNC\) = \(\Delta A´B´C´\) (1) por tener un lado congruente y los dos ángulos adyacentes.
como \(\Delta ABC \sim \) \(\Delta MNC\) (2) Teorema fundamental de existencia
Comparando (1) y (2), tenemos:
\(\Delta ABC \sim \) \(\Delta A´B´C´\)
Criterio 2: “Lado – ángulo – lado” (LAL)
Dos triángulos son semejantes cuando tienen, respectivamente dos de sus lados proporcionales y el ángulo formado por ellos congruentes.
Hipótesis: Sea \(\Delta ABC\) = \(\Delta A´B´C´\).
\(< BCA = < B´C´A´\)
\(\dfrac {\overline {AC}} {A´C´}=\dfrac {\overline {BC}} {\overline {B´C´}}\)
Tesis: \(\Delta ABC \sim \)\(\Delta A´B´C´\)
Demostración: Tomando \(\overline {CM}=\overline {C´A´}\) y tracemos \(\overleftrightarrow {MN}\parallel \overleftrightarrow {AB}\), formádonse el \(\Delta MNC\).
En \(\Delta MNC\) y \(\Delta A´B´C´\):
\(\overline {CM}=\overline {C´A´}\) / (1) por construcción.
<BCA = <B´C´A´ / por hipotesis
En los \(\Delta ABC\) y \(\Delta MNC\)
\(\dfrac {\overline {AC}} {MC}=\dfrac {\overline {BC}} {\overline {NC}}\) / (2) por construccion \(\overline {CM}=\overline {C´A´}\)
Sustituyendo (1) en (2), tenemos lo siguiente:
\(\dfrac {\overline {AC}} {A´C´}=\dfrac {\overline {BC}} {\overline {NC}}\) / (3)
pero como: \(\dfrac {\overline {AC}} {A´C´}=\dfrac {\overline {BC}} {\overline {B´C´}}\) / (4) Hipotesis
Comparando (3) y (4):
\(\dfrac {\overline {BC}} {NC}=\dfrac {\overline {BC}} {\overline {B´C´}}\) / por Transitividad
Despejando \(\overline {NC}=\dfrac {\overline {BC}.\overline {B´C´}} {\overline {BC}}\)
\(\overline {NC}=\overline {B´C´}\)
\(.:\Delta MNC = \Delta A´B´C´\) / por tener dos lados congruentes e igual ángulo comprendido.
Y como \(\Delta ABC \sim \Delta MNC\) / teorema fundamental de existencia
y \(\Delta MNC \sim \Delta A´B´C´\) /carácter idéntico.
Resulta \(\Delta ABC \sim \Delta A´B´C´\) /por transitividad.
Criterio 3: “Lado – lado - lado” (LLL)
Dos triángulos son semejantes cuando tienen sus tres lados, respectivamente, proporcionales.
Hipótesis: Sean \(\Delta ABC\) y \(\Delta A´B´C´\)
\(\dfrac {\overline {AB}} {\overline {A´B´}}=\dfrac {\overline {BC}} {\overline {B´C´}}=\dfrac {\overline {CA}} {\overline {C´A´}}\)
Tesis: \(\Delta ABC \sim \Delta A´B´C´\)
Demostración: Tomando \(\overline {CM}=\overline {C´A´}\) y tracemos \(\overleftrightarrow {MN}\parallel \overleftrightarrow {AB}\), formando \(\Delta MNC \sim \Delta ABC\)
Como: \(\dfrac {\overline {AB}} {\overline {MN}}=\dfrac {\overline {BC}} {\overline {NC}}=\dfrac {\overline {CA}} {\overline {CM}}\) / (1) por construcion \(\Delta ABC \sim \Delta MNC\)
Pero: \(\overline {CM}=\overline {C´A´}\) / (2) por construccion
Sustituyendo (2) en (1);
\(\dfrac {\overline {AB}} {\overline {MN}}=\dfrac {\overline {BC}} {\overline {NC}}=\dfrac {\overline {CA}} {\overline {C´A´}}\) / (3)
Pero:
\(\dfrac {\overline {AB}} {\overline {A´B´}}=\dfrac {\overline {BC}} {\overline {B´C´}}=\dfrac {\overline {CA}} {\overline {C´A´}}\) / (4) por hipotesis
Comparando (3) y (4):
\(\dfrac {\overline {AB}} {\overline {MN}}=\dfrac {\overline {BC}} {\overline {NC}}=\dfrac {\overline {AB}} {\overline {A´B´}}=\dfrac {\overline {BC}} {\overline {B´C´}}\) / por transitividad
Despejando \(\overline {MN}\): \(\overline {MN}=\dfrac {\overline {AB}.\overline {A´M´}} {\overline {AB}}\)
\(\overline {MN}=\overline {A´B´}\)
Tomando la 3era y la 4ta razón:
\(\dfrac {\overline {BC}} {\overline {NC}}=\dfrac {\overline {BC}} {\overline {B´C´}}\)
Despejando: \(\overline {NC}\): \(\overline {NC}=\dfrac {\overline {BC}.\overline {B´C´}} {\overline {BC}}\)
\(\overline {NC}=\overline {B´C´}\)
Entonces \(\overline {MN}=\overline {A´B´}\), \(\overline {NC}=\overline {B´C´}\) y \(\overline {CM}=\overline {A´C´}\) / Por construccion
\(.:\Delta MNC = \Delta A´B´C´\) / Por tener 3 lados congruentes.
y como \(\Delta ABC \sim \Delta MNC\) /Por teorema fundamental.
Resulta que el \(\Delta ABC \sim \Delta A´B´C´\)
2.0 Teoremas de Euclides
Para estudiar las relaciones métricas entre los elementos de los triángulos, es indispensable tener el concepto de proyección.
Definición: Se llama proyección de un punto P sobre una recta L, al pie P’ de la perpendicular bajada desde P a L.
La perpendicular PP’ se llama proyectante.
La proyección de un segmento AB sobre una recta L es el segmento A’B’, cuyos extremos son las proyecciones de los extremos A y B sobre L.
En la siguiente figura se representan las distintas proyecciones relativas de un segmento AB sobre una recta.
En ella podemos observar que si el segmento AB es paralelo a la recta, su proyección es igual a él. Si AB es perpendicular a la recta (último caso), la proyección se reduce a un punto A’ o B’.
Si en un triángulo rectángulo se traza la altura correspondiente a la hipotenusa, se verifica que:
Los triángulos rectángulos resultantes son semejantes entre sí y semejantes al triángulo dado.
\(\Delta ADC \sim \Delta BDC \sim \Delta ACB\)
2.1 Teorema de Euclides referente a la altura.
La altura correspondiente a la hipotenusa es media proporcional entre los segmentos de la hipotenusa

Se cumple: \(CD^{2}=AD\cdot BD\)
Demostración:
<ACD = <CBD
<CAD = <BCD
\(\Delta CBD \sim \Delta ACD \Rightarrow \dfrac {CD} {AD}=\dfrac {DB} {DC} \Rightarrow \dfrac {h} {q}=\dfrac {p} {h} \Rightarrow h^{2}=pq\)
2.2 Teorema de Euclides referente al cateto.
Cada cateto es media proporcional entre la hipotenusa y su proyección sobre ella.

Se cumple: \(AC^{2}=AB\cdot AD\)

Demostración:
<ACB = <ADC = 90°
<CAB = <DAC
Por criterio AA se tiene que:
\(\Delta ABC \sim \Delta ACD \Rightarrow \dfrac {AC} {AD}=\dfrac {AB} {AC} \Rightarrow \dfrac {b} {q}=\dfrac {c} {b} \Rightarrow b^{2}=qc\)

Se cumple que: \(BC^{2}=AB\cdot BD\)
Desmostración:

<ACB = <CDB = 90°
<CBA = <DBC
Por el Criterio AA se tiene que:
\(\Delta ABC \sim \Delta CBD \Rightarrow \dfrac {BC} {BD}=\dfrac {AB} {CB} \Rightarrow \dfrac {a} {p}=\dfrac {c} {a} \Rightarrow a^{2}=pc\)
3.0 Aplicación.
Este teorema se aplicaba para calcular alturas (árbol, montañas, edificios) cuando no existía el teodolito y fue base para la trigonometría. Siempre que se hallaba un obstáculo (río, quebradas, precipicios, montañas) y había que medir una distancia se utilizaban estas herramientas.
Euclides era capaz de dar aplicaciones prácticas a la geometría. Una vez, solicitaron a sus colegas de la Universidad de Alejandría que midieran la altura de la Gran Pirámide. Siendo imposible bajar una línea desde el ápice para medir la altura, quedaron perplejos. Empero Euclides ofreció una sencilla solución
geométrica.

Esperó hasta que llegara la hora del día en que su sombra midiera exactamente lo mismo que su estatura. Luego, midió la sombra de la pirámide y así determinó la altura de ésta.
Euclides, aplicó la semejanza de triágulos en el cálculo de distancias o alturas anaccesibles.
En fin, hay muchas utilidades que se le puede otorgar el teorema de Euclides.







Excelente trabajo Jesús.... me anima a buscar un buen tema
ResponderBorrarEspero tu trabajo amigo, saludos.
Borrargrasias en que programa se hacen los dibujos mil grasias y feliictaciones
ResponderBorrarGeogebra.
Borrar(Gracias)
Borrar