1.- Orígenes de la estadística.
El término
alemán Statistik, introducido originalmente por Gottfried Achenwall en 1749, se
refería al análisis de datos del Estado, es decir, la "ciencia del
Estado" (o más bien, de la ciudad-estado). También se llamó aritmética
política de acuerdo con la traducción literal del inglés. No fue hasta el siglo
XIX cuando el término estadística adquirió el significado de recolectar y
clasificar datos. Este concepto fue introducido por el militar británico Sir
John Sinclair (1754-1835).
En su origen,
por tanto, la Estadística estuvo asociada a los Estados o ciudades libres, para
ser utilizados por el gobierno y cuerpos administrativos (a menudo
centralizados). La colección de datos acerca de estados y localidades continúa
ampliamente a través de los servicios de estadística nacional e internacional.
En particular, los censos comenzaron a suministrar información regular acerca
de la población de cada país. Así pues, los datos estadísticos se referían
originalmente a los datos demográficos de una ciudad o estado determinados. Y
es por ello por lo que en la clasificación decimal de Chester Dewey empleada en
las bibliotecas, todas las obras sobre estadística se encuentran ubicadas al
lado de las obras de o sobre la demografía.
Desde los
comienzos de la civilización han existido formas sencillas de estadística, pues
ya se utilizaban representaciones gráficas y otros símbolos en pieles, rocas,
palos de madera y paredes de cuevas para contar el número de personas, animales
o ciertas cosas. Hacia el año 3000 a.C. los babilonios usaban ya pequeñas
tablillas de arcilla para recopilar datos en tablas sobre la producción
agrícola y de los géneros vendidos o cambiados mediante trueque.
Los egipcios
analizaban los datos de la población y la renta del país mucho antes de construir
las pirámides en el siglo XXXI a.C. Los libros bíblicos de Números y Crónicas
incluyen, en algunas partes, trabajos de estadística. El primero contiene dos
censos de la población de Israel y el segundo describe el bienestar material de
las diversas tribus judías. En China existían registros numéricos similares con
anterioridad al año 2000 a.C. Los griegos clásicos realizaban censos cuya
información se utilizaba hacia el 594 a.C. para cobrar impuestos.
El Imperio
romano fue el primer gobierno que recopiló una gran cantidad de datos sobre la
población, superficie y renta de todos los territorios bajo su control. Durante
la edad media sólo se realizaron algunos censos exhaustivos en Europa.
Los reyes
carolingios Pipino, el Breve, y Carlomagno ordenaron hacer estudios minuciosos
de las propiedades de la Iglesia en los años 758 y 762 respectivamente. Después
de la conquista normanda de Inglaterra en 1066, el rey Guillermo I de
Inglaterra encargó un censo. La información obtenida con este censo, llevado a
cabo en 1086, se recoge en el Domesday Book.
El registro de
nacimientos y defunciones comenzó en Inglaterra a principios del siglo XVI, y
en 1662 apareció el primer estudio estadístico notable de población, titulado
Observations on the London Bills of Mortality (Comentarios sobre las partidas
de defunción en Londres). Un estudio similar sobre la tasa de mortalidad en la
ciudad de Breslau, en Alemania, realizado en 1691, fue utilizado por el
astrónomo inglés Edmund Halley como base para la primera tabla de mortalidad.
En el siglo
XIX, con la generalización del método científico para estudiar todos los
fenómenos de las ciencias naturales y sociales, los investigadores aceptaron la
necesidad de reducir la información a valores numéricos para evitar la
ambigüedad de las descripciones verbales.
En nuestros
días, la estadística se ha convertido en un método efectivo para describir con
exactitud los valores de datos económicos, políticos, sociales, psicológicos,
biológicos y físicos, y sirve como herramienta para relacionar y analizar
dichos datos. El trabajo del experto estadístico no consiste ya sólo en reunir
y tabular los datos, sino sobre todo en el proceso de interpretación de esa
información.
2.- Conceptos Básicos.
La Estadística consiste en un conjunto de
técnicas y procedimientos que permiten recoger datos, presentarlos, ordenarlos
y analizarlos, de manera que a partir de ellos se puedan inferir conclusiones.
2.1.- Población.
La población
es un conjunto de objetos o de individuos que se desea estudiar y que, a su
vez, presentan una característica que interesa medir. Generalmente, el tamaño
de la población se denota con la letra N.
La población
puede ser según su tamaño de dos tipos:
a)
Población
finita: el número de elementos que la forman es finito, por ejemplo el
número de alumnos de un centro de enseñanza.
b)
Población
infinita: el número de elementos que la forman es infinito, o tan grande
que pudiesen considerarse infinitos. Como por ejemplo si se realizase un
estudio sobre los productos que hay en el mercado. Hay tantos y de tantas
calidades que esta población podría considerarse infinita.
Las personas o cosas que forman parte de
la población se denominan elementos.
En sentido estadístico un elemento puede ser algo con existencia real, como un
automóvil o una casa, o algo más abstracto como la temperatura, un voto, o un
intervalo de tiempo.
A su vez, cada elemento de la población
tiene una serie de características que pueden ser objeto del estudio
estadístico. Así por ejemplo si consideramos como elemento a una persona,
podemos distinguir en ella los siguientes caracteres:
Sexo, Edad, Nivel de estudios, Profesión, Peso, Altura, Color de pelo, etc.
2.2.- Muestra.
Se llama muestra
a un subconjunto representativo de la población que se desea estudiar.
Generalmente, el tamaño de la muestra se denota con la letra n.
2.3.- Variables.
Una variable
estadística corresponde a la o las características que se miden en la muestra.
Las variables pueden ser cuantitativas,
si se pueden medir numéricamente, o cualitativas,
si no, es decir, si sus valores son etiquetas que representan categorías o
cualidades.
Una variable
cuantitativa puede ser discreta, cuando
los posibles valores surgen frecuentemente de un conteo, o continua, cuando los posibles valores surgen frecuentemente de una
medición, luego, puede tomar tantos valores como sea posible.
2.3.1 Variables según su medición.
La medición es
el proceso mediante el cual se le asignan valores numéricos a objetos siguiendo
determinadas reglas. Los instrumentos que se utilizan para ello se denominan
escala de medición, los cuales son la nominal, la ordinal, la de intervalo y la
de razón.
El Nivel de medición nominal son los
datos consistentes exclusivamente en nombres, etiquetas o categorías que no
pueden acomodarse según un esquema de orden (por ejemplo, de bajo a alto).
Los datos
están en el nivel de medición ordinal
cuando pueden acomodarse en algún orden, aunque no es posible determinar
diferencias entre los valores de los datos o tales diferencias carecen de significado.
El nivel de medición de intervalos se
parece al nivel ordinal, pero con la propiedad adicional de que la diferencia
entre dos valores de datos cualesquiera tiene un significado. Sin embargo, los
datos en este nivel no tienen un punto de partida inherente (natural) desde
cero (donde nada de la cantidad esté presente).
El nivel de medición de razón se parece al
nivel de intervalo, aunque tiene la propiedad adicional de que sí tiene un
punto de partida o cero inherente (donde cero indica que nada de la cantidad
está presente). Para valores en este nivel, tanto las diferencias como las
proporciones tienen significado.
3. Ordenamiento de
información.
Una vez que
hemos observado y recogidos los datos, bien a través de encuestas, bien con
bases de datos ya almacenados, debemos resumir la información de forma adecuada
y útil para su posterior estudio.
Una vez
realizado el recuento de datos interesa recoger la información de la muestra
resumida en una tabla en la que a cada valor de la variable se le asocian
determinados números que representan el número de veces que ha aparecido, su
proporción con respecto a otros valores de la variable, etc. Estos números se
denominan frecuencias: Así tenemos los siguientes tipos de frecuencia:
Frecuencia absoluta: La frecuencia
absoluta de una variable estadística es el número de veces que aparece en la
muestra dicho valor de la variable, la representaremos por ni.
Frecuencia relativa: La frecuencia
absoluta, es una medida que está influida por el tamaño de la muestra, al
aumentar el tamaño de la muestra aumentará también el tamaño de la frecuencia
absoluta. Esto hace que no sea una medida útil para poder comparar. Para esto
es necesario introducir el concepto de frecuencia relativa, que es el cociente
entre la frecuencia absoluta y el tamaño de la muestra. La denotaremos por fi
Porcentaje: La frecuencia relativa es
un tanto por uno, sin embargo, hoy día es bastante frecuente hablar siempre en
términos de tantos por ciento o porcentajes, por lo que esta medida resulta de
multiplicar la frecuencia relativa por 100. La denotaremos por pi.
Frecuencia Absoluta Acumulada: Para
poder calcular este tipo de frecuencias hay que tener en cuenta que la variable
estadística ha de ser cuantitativa. Es el número de veces que ha aparecido en
la muestra un valor menor o igual que el de la variable y lo representaremos
por Ni.
Frecuencia Relativa Acumulada: Al igual
que en el caso anterior la frecuencia relativa acumulada es la frecuencia
absoluta acumulada dividido por el tamaño de la muestra, y la denotaremos por Fi.




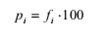


No hay comentarios.:
Publicar un comentario
Se prohibe comentarios ofensivos, insultos o spam. Los comentarios están bajo una moderación.